Taxonomie de l'apprentissage automatique (machine learning)

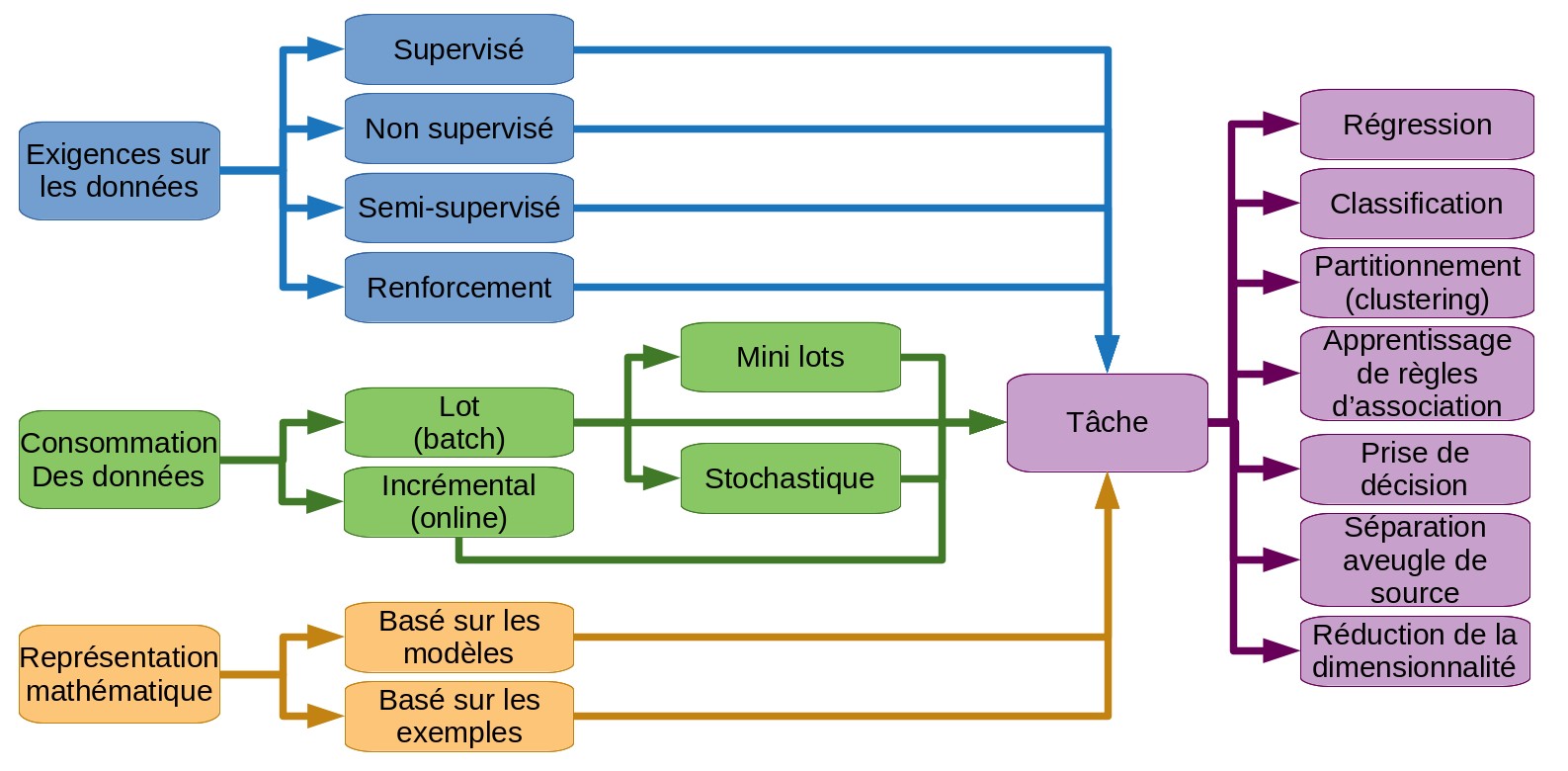
Introduction

Dans le précédent article de cette série consacrée à l’apprentissage automatique, j’ai essayé d’exprimer clairement ma compréhension de l’apprentissage automatique (machine learning). J’y soutenais que je conçois l’apprentissage automatique comme un ensemble d’algorithmes et de méthodes permettant de déterminer automatiquement les paramètres de modèles mathématiques et de choisir automatiquement le modèle plus adapté à un problème donné.

Dans cet article je vais essayer présenter brièvement ma taxonomie personnelle (taxonomie = catégorisation) des techniques d’apprentissage automatique. J’espère que cette présentation nous fournira dans le même temps une vue générale des usages courants de l’apprentissage automatique.

Un clic sur l’icône de table des matières à droite permet d’avoir une vue hiérarchique de la taxonomie à tout moment. Je suggère également d’ouvrir les liens internes dans de nouveaux onglets afin de ne pas perdre votre position de lecture dans l’article.

Taxonomie par les exigences sur l’ensemble de données

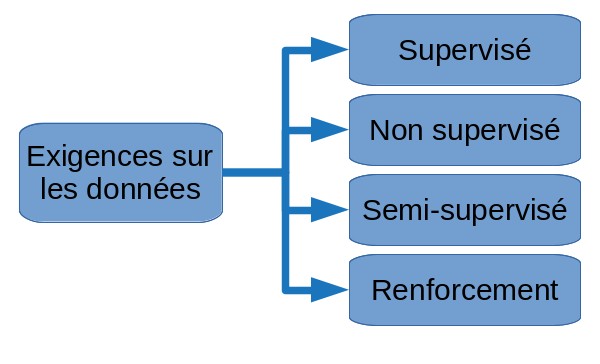
En fonction des données disponibles et de l’objectif du logiciel que nous développons, nous allons entraîner nos modèles différemment. Dans les sections qui suivent nous discuterons de l’apprentissage supervisé où des exemples de résultats attendus sont présents, l’apprentissage non supervisé où aucun exemple de résultat n’est fourni et l’apprentissage par renforcement où la donnée est collectée par interaction avec un environnement.

Apprentissage supervisé

Un algorithme d’apprentissage supervisé nécessite la présence, pendant la phase d’apprentissage, des résultats corrects attendus pour chaque élément de l’ensemble initial de données. Nous dirons dans ce cas que les éléments sont annotés ou étiquetées.

Illustration de l'apprentissage supervisé. L'algorithme va apprendre à partir des images étiquetées de chiens et de chats. L'image dans le coin inférieur droit est la nouvelle entrée qu'il devra étiqueter.

Par exemple, supposons que mon ensemble de données soit ma boîte mail. Supposons que j’ai pour habitude de trier manuellement mes emails en tant que “spam” ou “pas spam”. Supposons à présent que je veuille créer un logiciel pour filtrer automatiquement mes emails à ma place. Dans cette configuration, j’ai des exemples à fournir à mon algorithme d’apprentissage : les emails triés manuellement. J’ai donc les entrées de mon futur algorithme (les emails) mais aussi les sorties correspondantes (qu’ils soient “spam” ou “pas spam”). Un algorithme qui se base sur un tel type données pour l’apprentissage est dit supervisé. Il nécessite des entrées et les sorties correspondantes. C’est à partir des ces exemples que l’algorithme va trouver la meilleure fonction de prédiction pour de nouvelles données.

Une analogie de l’apprentissage supervisé est souvent faite avec la situation où nous montrons un objet à un enfant et nous ennoncons le nom de l’objet de sorte que l’enfant apprenne à nommer cet objet.

Apprentissage non supervisé

Contrairement à l’apprentissage supervisé, une technique d’apprentissage non supervisé ne nécessite pas la présence d’exemples de resultats attendus (ou d’étiquettes).

Illustration de l'apprentissage non supervisé. Les zones colorées montrent un regroupement d'images non étiquetées de chiens et de chats. L'algorithme met dans le même groupe les images présentant des caractéristiques similaires.

Par exemple, supposons que j’aie une base de données qui contienne l’historique, sur une décennie, des achats faits par des utilisateurs sur un site de vente en ligne. Supposons que je veuille créer un système de recommandation automatique de produits pour ce site. Mon but est, étant donné un produit que l’utilisateur est en train de visualiser, de lui suggérer un autre produit qui a le maximum de chances d’être acheté en même temps que celui en cours de consultation. Intuitivement, nous pourrions par exemple proposer à l’utilisateur des couches pour bébé s’il est en train de consulter le détail d’un biberon. Je souhaite que mon algorithme d’apprentissage découvre automatiquement ce type d’associations dans mon ensemble de données.

Dans cet exemple je n’avais aucun résultat correcte sur lequel baser l’apprentissage. J’avais uniquement les entrées, c’est-à-dire les transactions présentes dans ma base de données. Plus loin dans cet article nous discuterons de l’apprentissage de règles d’associations, un ensemble de techniques d’apprentissage non supervisé conçues justement pour extraire ce type de relations d’une base de transactions.

Apprentissage semi-supervisé

Je conçois l’apprentissage semi-supervisé comme un apprentissage non supervisé renforcé par un apprentissage supervisé.

L’apprentissage semi-supervisé est généralement utilisé lorsque nous avons une petite quantité d’entrées étiquetées et beaucoup plus d’entrées non étiquetées.

Illustration d'un algorithme semi-supervisé. Une phase non-supervisée regroupe les images non étiquetées de chiens et de chats (zones colorées). Une phase supervisée peut alors étiqueter tous les chats comme "chat" et tous les chiens comme "pas chats", en se basant sur l'unique image étiquetée en haut à gauche.

Par exemple, reformulons notre exemple de filtrage d’emails afin que seuls $20$ e-mails sur $20 000$ soient triés dans les $2$ dossiers comme spam ou pas spam . La plupart des algorithmes d’apprentissage supervisé entraînés uniquement sur les $20$ emails fonctionneront mal sur l’ensemble beaucoup plus volumineux de courriers non triés. Une solution peut consister à exécuter un algorithme non supervisé qui regrouperait les courriers similaires ($2$ groupes dans notre cas). Cet algorithme de regroupement s’appliquerait à l’ensemble des données ($20000 + 20$ emails). Ensuite, nous assignerions à tout courrier électronique non trié le dossier de son plus proche voisin (selon une certaine métrique) parmi les $20$ emails triés et qui seraient dans le même groupe. Plus clairement, désignons un e-mail par un nombre compris entre $1$ et $20020$, où $1$ à $20$ désignent les e-mails triés. Si, par exemple, le courrier électronique $2$ (qui figure parmi les $20$ courriers électroniques triés) est à la distance la plus courte d’un courrier quelconque désigné par $i$ et si le courrier $2$ est un spam, nous considérerions alors que le courrier $i$ est également un spam.

Dans cet exemple, nous avons en fait utilisé deux algorithmes non supervisés: le premier pour créer les groupes est un algorithme de partionnement (ou clustering) et le second pour trouver le plus proche voisin est un algorithme de classification , 2 taxons dont nous discutons plus loin.

Il me faut mentionner que le point de vue inverse est également vrai - voir l’apprentissage semi-supervisé comme un apprentissage supervisé renforcé par un apprentissage non supervisé - où l’apprentissage non supervisé peut être considéré comme un pré-traitement.

Enfin, nous noterons que l’apprentissage semi-supervisé est souvent utilisé dans des configurations où la collecte de données est facile mais l’étiquetage est coûteux (généralement en temps).

Apprentissage par renforcement

L’apprentissage par renforcement ne requiert pas un ensemble initial de données, mais plutôt un environnement (ou un contexte). Les données sont collectées par l’algorithme d’apprentissage en explorant l’environnement. L’algorithme tente d’optimiser un processus de décision vers un objectif.

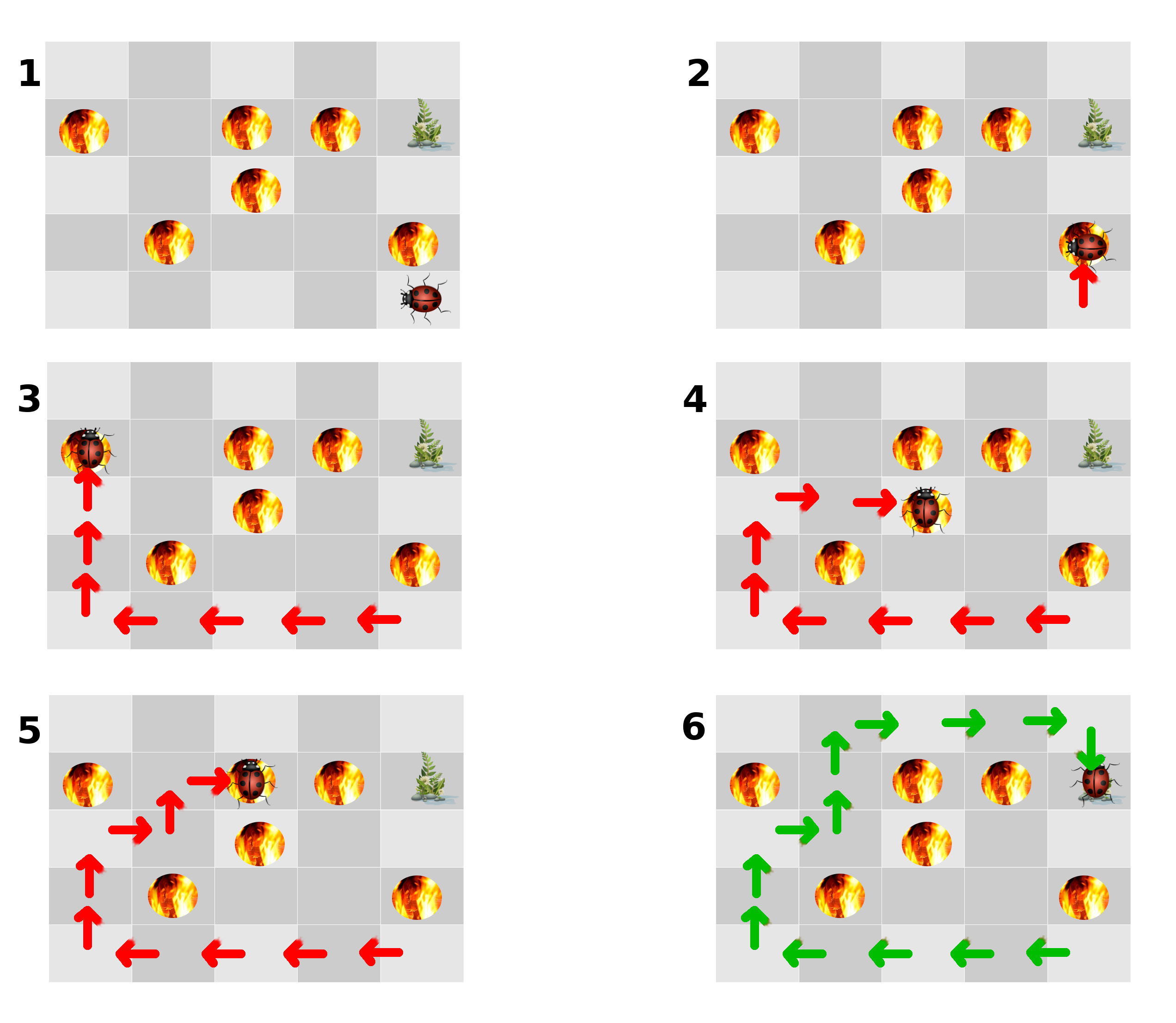Illustration de l'apprentissage par renforcement. L'algorithme explore l'environnement et apprend à atteindre son objectif (atteint dans l'image 6).

Les problèmes adressés par l’apprentissage par renforcement comprennent l’optimisation du comportement des agents autonomes, la prise de décision pour les investissements boursiers, l’optimisation des itinéraires, les stratégies de jeu, les stratégies commerciales, etc.

Taxonomie par les représentations mathématiques

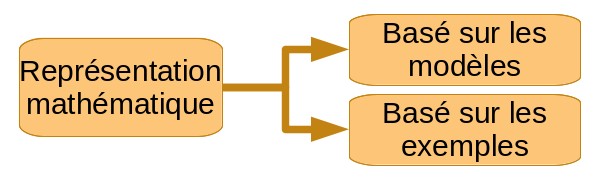
Certaines techniques d’apprentissage automatique ne font que comparer les nouvelles données à celles sur lesquelles elles ont été entraînées. D’autres essaient de trouver une représentation générale des relations existant dans l’ensemble de données. Les premières sont dites basées sur des exemples, les secondes basées sur des modèles.

Apprentissage basé sur les exemples (ou à memoire)

Pour faire des estimations, une fonction de prédiction obtenue par un apprentissage basé sur les exemples compare les nouvelles données aux exemples rencontrés durant l’apprentissage.

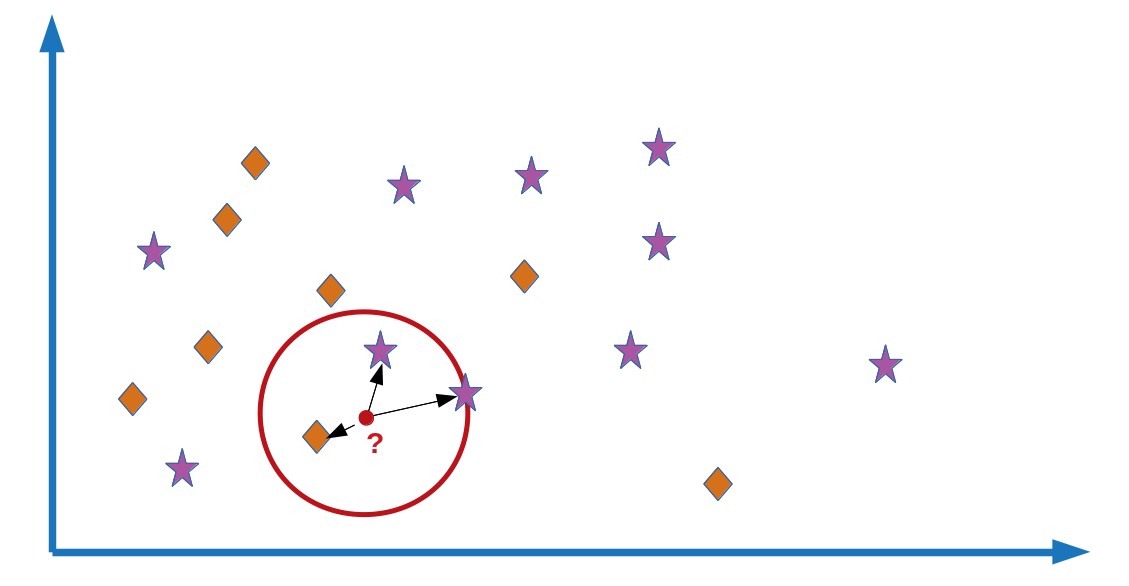Illustration de l'apprentissage basé sur les exemples. Le point rouge est la "nouvelle" entrée à classer. Ses plus proches voisins se situent dans le cercle rouge. Il sera classé comme "étoile" parce que cette étiquette est la plus commune parmi ses plus proches voisins.

Généralement, une métrique ou parfois une mesure de similarité est nécessaire. Les métriques incluent la distance euclidienne, la distance de Hamming, la distance de Levenshtein (utilisée pour la comparaison de texte), etc.

Parmis les stratégies pour estimer la valeur de la propriété d’intérêt pour de nouvelles données nous pouvons citer le “vote” et la moyenne. Le vote signifie que l’estimation fournie par la fonction de prédiction sera égale à la valeur la plus courante parmi les $k$ exemples d’apprentissage les plus proches de la nouvelle donnée (selon la métrique choisie). La moyenne signifie que la fonction de prédiction fournie comme estimation la valeur moyenne de la propriété d’intérêt des $k$ plus proches voisins. Dans le cas de la moyenne, si $k = 1$, il s’agit simplement la valeur du plus proche voisin.

Dans notre exemple de filtrage d’emails par apprentissage semi-supervisé, la phase non supervisée dans laquelle nous trions les $20000$ courriers non étiquetés “en les comparant simplement” aux $20$ courriers étiquetés est un exemple de technique basée sur les exemples.

Apprentissage basé sur les modèles

Un algorithme d’apprentissage basé sur les modèles tente de généraliser à partir des exemples d’apprentissage qui lui ont été fournis. La représentation mathématique que l’algorithme obtient à partir de ce processus de généralisation est le modèle qui sera utilisé pour effectuer des estimations sur de nouvelles données.

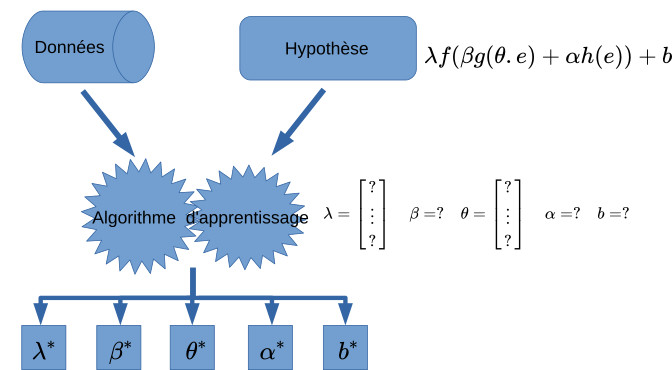Illustration de l'apprentissage basé sur les modèles. L'algorithme sélectionne une hypothèse, une représentation mathématique. Ensuite, il en détermine les paramètres en fonction des données disponibles.

Notre discussion pour obtenir une intuition de l’apprentissage automatique nous a donné (je l’espère) une bonne idée de ce qu’est l’apprentissage basé sur les modèles.

Taxonomie par modes d’approvisionnement en données d’apprentissage

Intuitivement, nous sentons que les techniques d’apprentissage automatique ne devraient pas garder en mémoire l’ensemble des données sur lesquelles elles ont été entraînées. Or les ajustements itératifs effectués par la méthode d’apprentissage sur la représentation mathématique qu’elle tente de déterminer sont basés sur les données qui lui sont fournies. Pour ces raisons antagonistes, nous pouvons comprendre intuitivement que de nombreuses techniques d’apprentissage ne pourront pas, sur de nouvelles données, ajuster davantage une fonction de prédiction déjà déterminée, tout en la maintenant cohérente avec son apprentissage précédent (car il n’y a pas de mémoire des données précédentes).

Les techniques d’apprentissage nécessitant l’intégralité du jeu de données lors de la phase d’apprentissage sont appelées méthodes d’apprentissage par lots. Toutefois, il existe certains algorithmes d’apprentissage capables d’ajuster, sur de nouvelles données, une fonction de prédiction étant déjà passée par une phase d’apprentissage. On les appelle méthodes d’apprentissage incrémental.

Apprentissage par lots (batch learning)

Dans l’apprentissage par lots, tous les exemples doivent être fournis pendant la phase d’apprentissage. La “fonction de prédiction” résultant de l’apprentissage est ensuite utilisée en production et l’apprentissage est définitivement terminé pour cette fonction de prédiction.

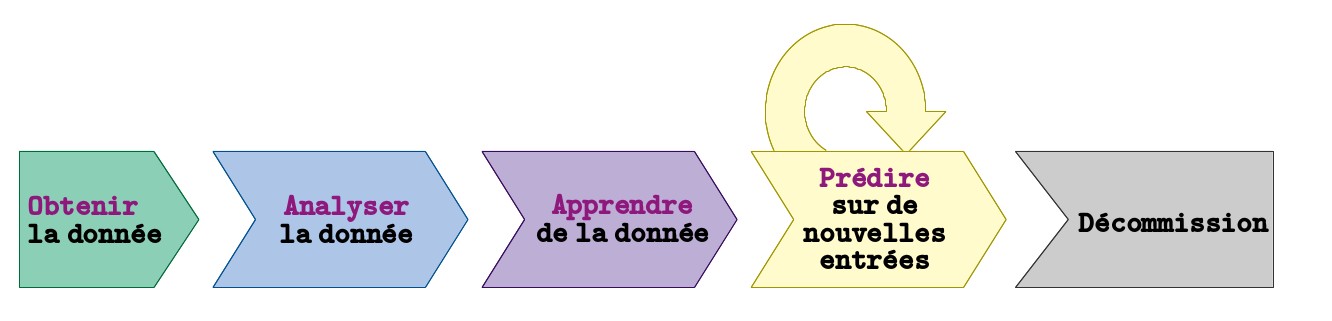
Dans ce contexte, si nous obtenons de nouveaux exemples, nous devons refaire l’apprentissage sur un nouveau modèle, à partir de zéro, sur l’ensemble complet et enrichi de données.

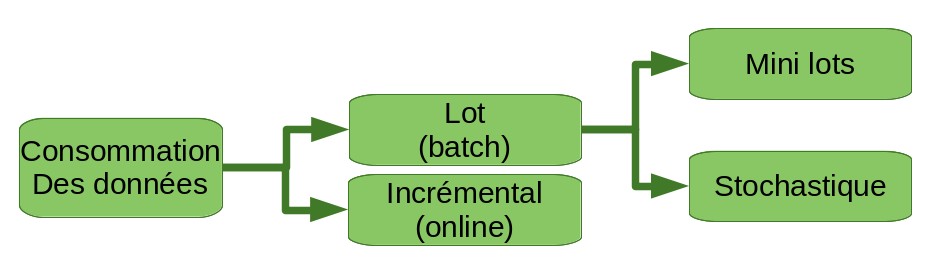
Pour les grands ensembles de données qui ne peuvent pas tenir entièrement dans la mémoire d’un ordinateur, certaines techniques existent pour réaliser l’apprentissage par lots. Ce sont les méthodes out-of-core. Certaines d’entre elles abordent le problème au niveau de l’accès aux données et de leur gestion, en permettant par exemple de charger en mémoire uniquement le sous-ensemble de données nécessaires à un calcul à un instant $t$. Cela nécessite en général une transformation des données vers une représentation qui facilite ces optimisations. D’autres techniques sont des variantes d’algorithmes d’apprentissage par lots permettant d’accepter les données par plus petits lots. Ces techniques de mini-lots (mini-batchs) nécessitent toujours l’ensemble des données au moment de l’apprentissage, mais les “consomment” par petits sous-ensembles. Enfin, les méthodes stochastiques (aleatoires) consomment un élément à la fois et sélectionnent cet élément suivant une distribution de probabilité.

Apprentissage incrémental (online learning)

Contrairement à l’apprentissage par lots, une technique d’apprentissage incrémental peut être alimentée progressivement avec de nouveaux éléments et modifie ses représentations en conséquence, même lors de son utilisation en production.

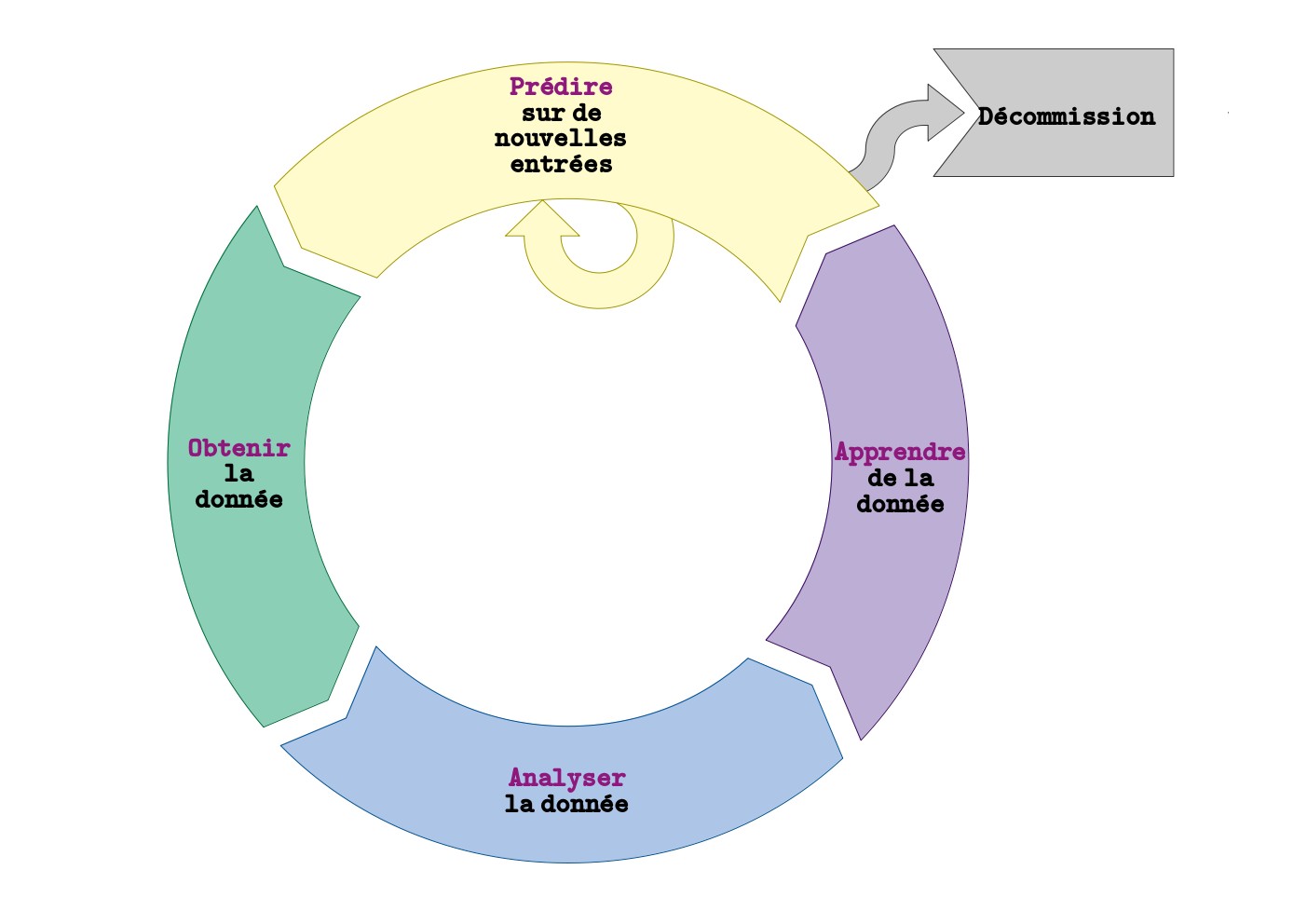
Un algorithme d’apprentissage incrémental utilise la fonction de prédiction courante comme input supplémentaire, en plus des données.

Pour de nombreuses représentations sous-jacentes, un véritable apprentissage incrémental n’est pas possible. Cependant, en fonction de la formulation, on peut souvent trouver un pseudo-algorithme incrémental basé sur un algorithme récursif. Dans ce cas, la nouvelle fonction de prédiction dépend de la meilleure fonction actuelle et de tous les exemples précédents (déjà appris) en plus des nouveaux. Dans certains cas, la dépendance par rapport aux exemples précédents peut être exprimée à l’aide d’une fonction d’agrégation. Dans ce cas, nous ne stockons pas réellement ces éléments, mais plutôt la fonction d’agrégation et les informations nécessaires à son calcul (y compris son résultat précédent). Lorsqu’aucune astuce de ce type n’est possible, aucune garantie ne peut être donnée sur la complexité de stockage ou de mémoire des algorithmes récursifs pseudo-incrémentaux.

Taxonomie par l’usage ou l’objectif

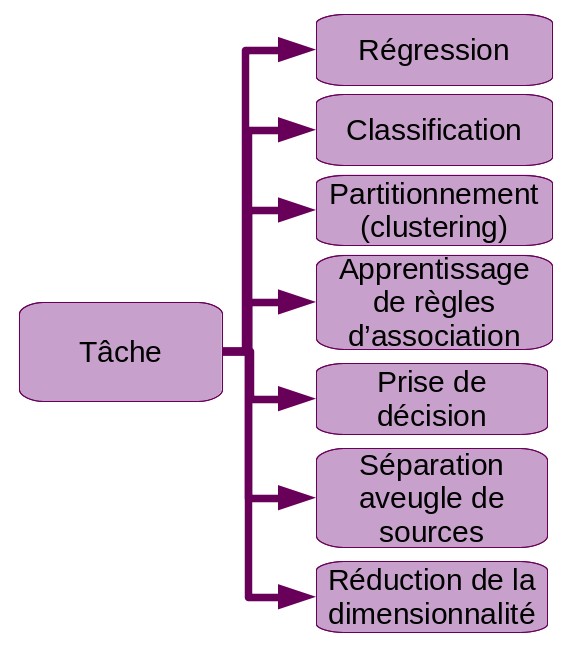
Parmis les tâches d’apprentissage automatique les plus répandues nous retrouvons:

• Trouver la valeur d’une propriété d’un phénomène qui dépend des valeurs d’autres propriétés de ce phénomène (ou d’autres instances du phénomène). Il s’agit de la régression.

• Rechercher des frontières pour séparer les éléments de données en groupes. Lorsque les groupes sont imposés dès le départ (ils font partie des entrées de l’algorithme), la tâche est appelée classification. Lorsque les groupes doivent être déterminés par l’algorithme, nous appelons la tâche partitionnement (ou clustering).

• Optimiser les processus de décision.

• Découvrir des règles d’association (apprentissage de règles d’association).

• Désassembler une mesure (souvent une série temporelle) en ses composantes basiques. C’est la séparation aveugle de sources.

• Réduire le nombre de variables d’entrée d’un problème d’apprentissage. Cette tâche est appelée réduction de la dimensionnalité.

Régression

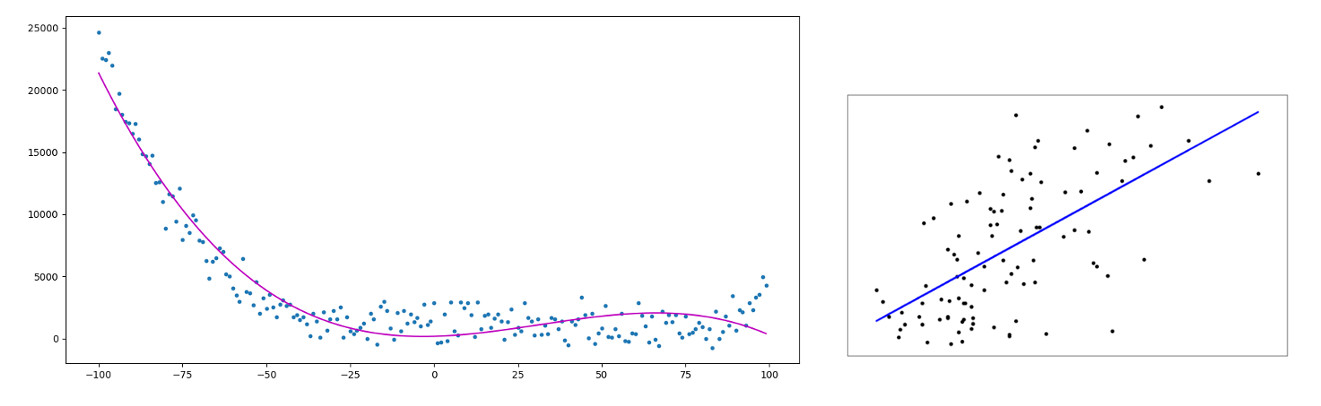Illustration de la régression. Les données d'entrée ont seulement 1 caractéristique. A gauche, une régression polynomiale de degré 3 et à droite, une régression linéaire.

La régression tente de trouver la valeur d’une propriété d’un phénomène en fonction des valeurs d’autres propriétés ou d’instances du même type.

La régression est généralement une tâche d’apprentissage supervisé.

Par exemple, supposons qu’un vendeur de crèmes glacées veuille prédire ses revenus en fonction de la température qu’il fera. Nous ferions l’apprentissage des paramètres (et d’un modèle) d’une régression si nous essayions de créer un logiciel satisfaisant cette exigence.

Classification

La classification tente de trouver des frontières dans le jeu de données afin de séparer les éléments en un certain nombre de classes connues (ou définies) avant l’apprentissage.

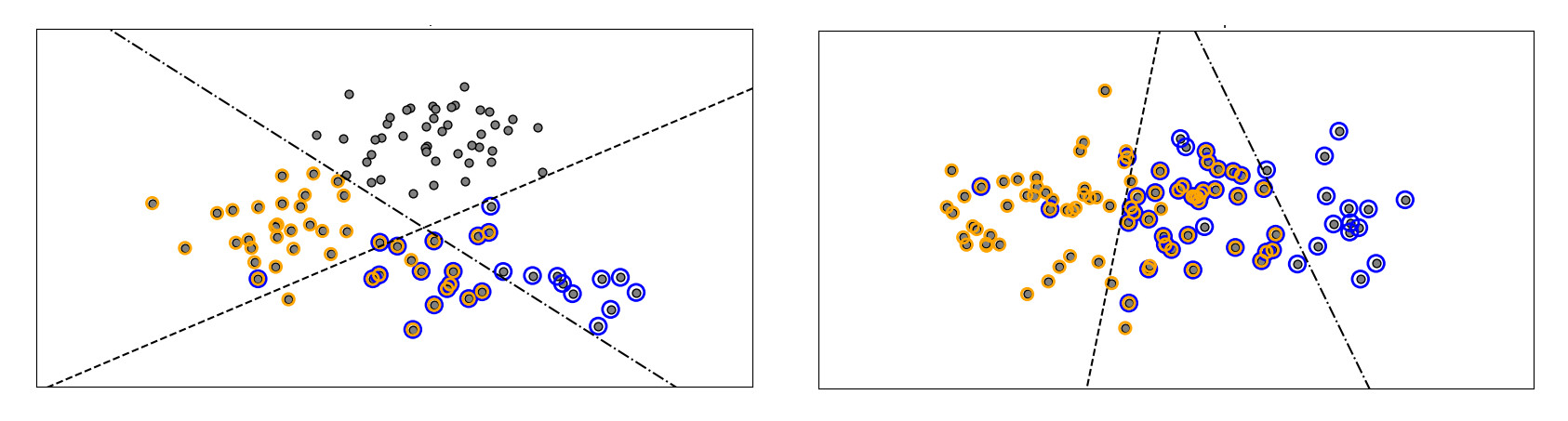Illustration de la classification. Les deux modèles illustrés sur l'image tracent des frontières linéaires (les données sont linéairement séparables). Crédit: [1]

La classification est typiquement une activité d’apprentissage supervisé.

Par exemple, si nous avions un ensemble de données étiquetées comprenant des images de chiffres manuscrits allant de $0$ à $9$, l’apprentissage d’une fonction permettant de reconnaître les chiffres sur de nouvelles images constituerait une tâche de classification dans laquelle les classes seraient $1, 2, \dots, 9$. Par ailleurs, notre exemple de filtrage d’e-mails est une tâche de classification avec deux classes: spam ou pas spam.

Pour moi la classification est une tâche conceptuellement bien différente de la régression, mais certains auteurs les présentent comme similaires. Pour ces auteurs, la seule différence est que le résultat de la régression est continu tandis que le résultat de la classification est discret et fini. Je ne partage pas totalement cette vision, car comme je le disais ci-dessus, je conçois la régression comme tentant d’estimer une valeur tandis la classification tente d’estimer une frontière.

Partitionnement (clustering)

Le partitionnement tente de regrouper les observations de sorte que les éléments appartenant au même groupe (ou partition) soient plus similaires - selon une certaine mesure de similarité - et ceux appartenant à des groupes différents soient plus dissemblables.

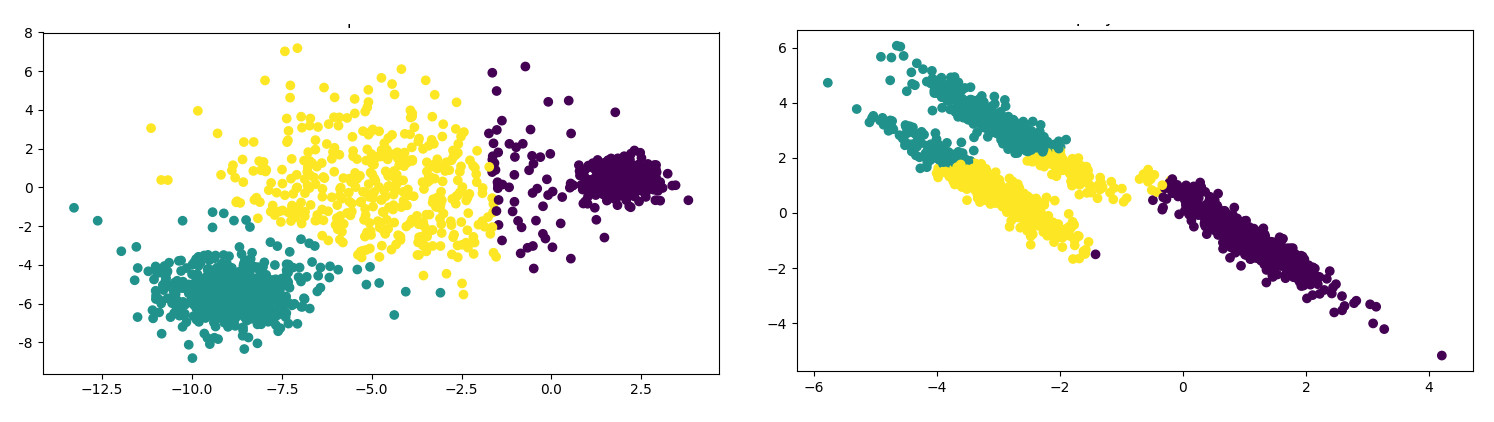Illustration du partitionnement. Le graphique représente les partitions avec des couleurs. Crédit: [2]

Les algorithmes de partionnement résultent typiquement d’apprentissages non supervisés.

Nous avons présenté un cas de partionnement en parlant d’apprentissage semi-supervisé via notre exemple modifié de filtrage de courrier électronique. Dans la vraie vie, les algorithmes de partionnement aident les biologistes à etablir leurs taxonomies, les spécialistes du marketing à trouver des groupes de clients partageant les mêmes comportements, les moteurs de recherche dans la catégorisation des pages Web…

Prise de décision

Un algorithme de prise de décision essaie de trouver quelles actions effectuer afin d’optimiser un gain, l’utilisation d’une ressource ou l’évolution vers un objectif.

Illustration de l'apprentissage par renforcement. En explorant l'environnement, l'algorithme apprend quelles décisions prendre pour atteindre son objectif.

L’apprentissage de la prise de décisions optimales peut être aussi bien supervisé, semi-supervisé ou par renforcement. Cependant, cette tâche est souvent associée à l’apprentissage par renforcement.

L’apprentissage automatique pour la prise de décision est utilisé pour le trading en bourse, la construction d’agents autonomes (comme les rovers explorant la planète Mars), les stratégies de jeu, la prise de décision en politique, en assurance et dans bien d’autres domaines où la stratégie est importante.

Apprentissage de règles d’association

L’apprentissage de règles d’association tente de déterminer la manière dont des acteurs associent des éléments.

Illustration de l'apprentissage de règles d'association. Les règles sur cet exemple représentent les associations de produits souvent présentes dans les chariots des clients dans un magasin. Les clients qui achètent du lait et des couches achètent souvent du pain :)

La différence conceptuelle fondamentale avec le partionnement réside, à mon avis, dans le fait que le partionnement se base sur les propriétés des éléments pour les regrouper, tandis que l’apprentissage de règles d’association se base sur la manière dont d’autres agents ou acteurs regroupent les éléments dans certaines transactions.

L’apprentissage de règles d’association est typiquement réalisé de manière non supervisée.

Nous avions donné un exemple d’apprentissage de règles d’association dans notre discussion sur l’apprentissage non supervisé plus haut. D’autres usages des algorithmes obtenus par apprentissage de règles d’association sont notamment le placement des livres dans une bibliothèque, la disposition des produits dans un magasin, la composition des packs de services (d’assurance par exemple)…

Une analogie de l’apprentissage de règles d’association peut être faite avec la manière dont nous déchiffrons une langue ancienne. Connaissant les structures de bases communes à toutes les langues, les relations entres elles (ascendance, similarités, etc.), d’autres propriétés statistiques et certains faits historiques, nous apprenons les règles d’association des anciens utilisateurs de la langue de sorte que les scripts qu’ils ont laissé aient du sens pour nous.

Séparation aveugle de sources

La séparation aveugle de sources tente de décomposer une mesure en ses composantes de base. Généralement, la mesure est une série chronologique, comme un enregistrement sonore.

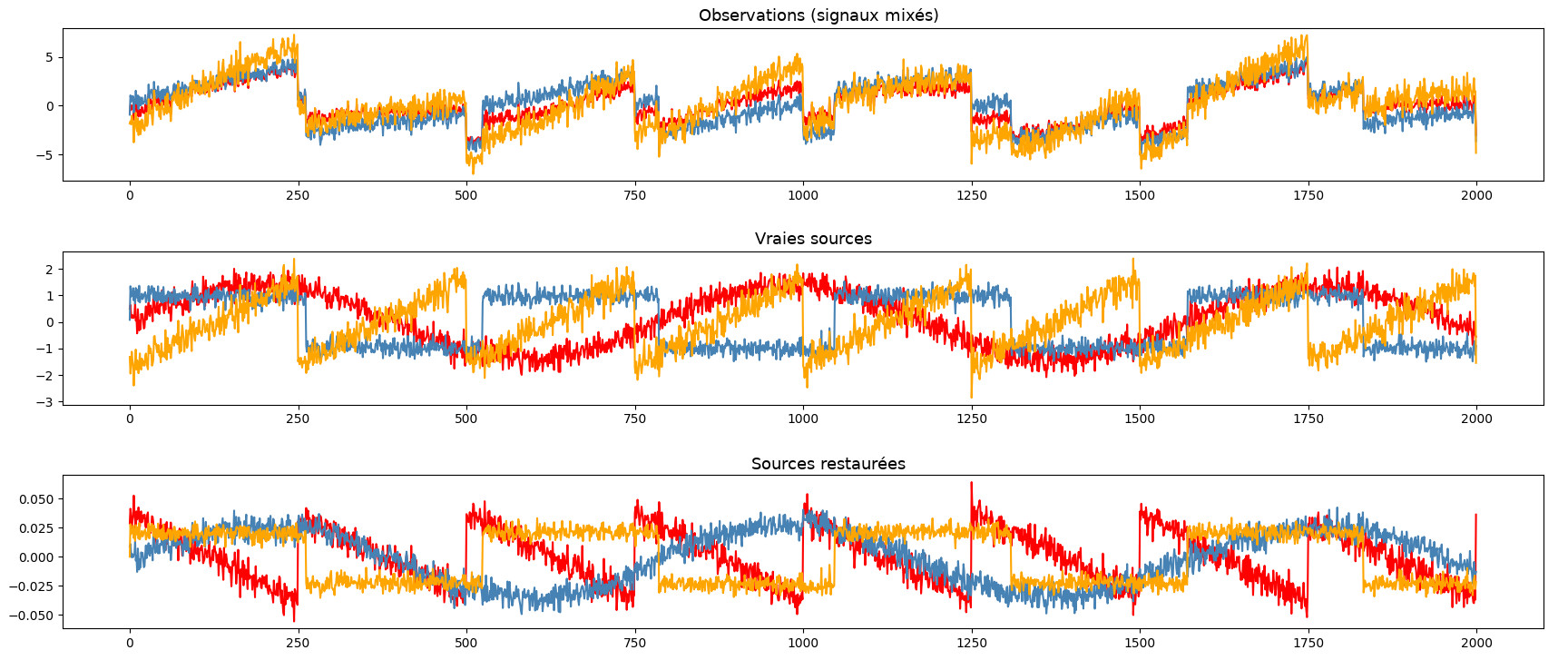Illustration de la séparation aveugle de sources. Les signaux sont correctement récupérés (l'image du bas) mais les couleurs diffèrent. Ceci illustre l'aspect "aveugle" de l'algorithme, qui ne sait rien des signaux initiaux (image du milieu). Credit: [3]

La séparation aveugle de sources est souvent décrite sous forme non supervisée, mais elle peut également être supervisée.

Un exemple souvent cité de séparation aveugle de sources consiste à détacher les discours de personnes différentes d’un enregistrement sur lequel elles parlent toutes en même temps. Imaginons que nous soyons à une fête et que nous allions dans la cuisine où cinq personnes parlent en même temps. Nous enregistrons cette cacophonie et souhaitons séparer le discours de chaque personne sur une piste différentes. Ceci serait une tâche pour la séparation aveugle de sources. Ici, “aveugle” signifie que l’algorithme n’a aucune information sur la source des signaux, ni sur le processus de mixage.

Une analogie de la séparation aveugle de sources est la façon dont nous, humains, dans une foule où plusieurs personnes parlent en même temps, sommes capables d’isoler la voix de quelqu’un en particulier que nous voulons écouter.

Réduction de la dimensionnalité

La réduction de la dimensionnalité tente de réduire le nombre de variables d’entrée d’un problème d’apprentissage tout en conservant autant d’informations pertinentes que possible.

Illustration de la réduction de la dimensionnalité. Chaque image représente un chiffre manuscrit. La sélection et l'extraction de caractéristiques ont donné ces images pixellisées en niveaux de gris. Il s'avère que l’algorithme de classification fonctionne très bien sur cet ensemble réduit de données. Crédit: [4]

Le résultat de la réduction de dimensionnalité peut être utilisé comme entrée d’autres algorithmes d’apprentissage ou pour de la visualisation (si le nombre d’entrées peut être réduit à $3$ ou moins). Utilisé comme entrée d’autres algorithmes d’apprentissage, cela peut améliorer leurs performances (réduire leurs erreurs de généralisation) car moins de variables signifie souvent des algorithmes d’apprentissage moins complexes, moins de bruit et moins de redondance dans les données.

Les variables d’entrée des algorithmes d’apprentissage sont appelées caractéristiques. Généralement, la réduction de la dimensionnalité consiste en 3 types de réduction de caractéristiques:

• La sélection de caractéristiques tente de trouver un sous-ensemble de caractéristiques les plus pertinentes pour un problème donné.
• L’extraction de caractéristiques est souvent utilisée en conjonction avec la sélection de caractéristiques et tente d’inférer de nouvelles caractéristiques à partir de celles existantes. On espère ainsi que ces nouvelles caractéristiques seront plus informatives et moins redondantes que les caractéristiques initiales, tout en décrivant toujours avec précision l’ensemble initial de données.
• La projection de caractéristiques réduit la dimension des entrées en les projetant sur “une géométrie” de dimension inférieure. La projection de caractéristiques est utile lorsque nous supposons que les entrées sont décrites par une “geométrie” de dimension inférieure, mais repliée dans un espace de dimension supérieure. Par exemple, dans l’image ci-dessous, les entrées en forme de S à gauche constituent une surface 2D “pliée” dans un espace 3D.

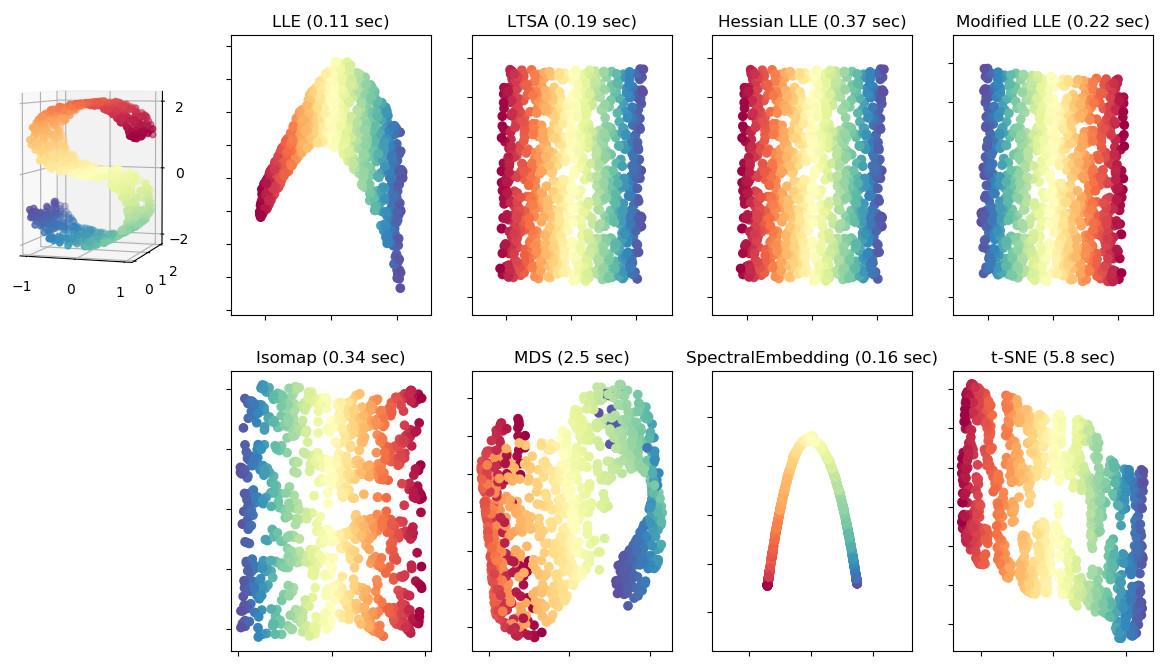Illustration de la projection de caractéristique. Diverses projections sur un plan d'une surface 2D pliée en 3D. Crédit: [5]

Nous devons noter que l’un des grands défis de l’apprentissage automatique consiste parfois à trouver ou à choisir la représentation de nos caractéristiques. Par exemple, dans notre exemple de filtrage de courrier électronique, comment pourrions-nous représenter numériquement un courrier électronique, de sorte qu’il constitue une entrée pertinente pour un algorithme d’apprentissage ? Une méthode peut consister à: 1) créer un “dictionnaire” contenant tous les mots apparaissant dans tous les emails, 2) représenter un courrier par un vecteur où chaque composante est l’indice du mot dans le dictionnaire. Une autre option peut-être que chaque composante du vecteur est le nombre d’occurrences dans l’email de chaque mot du dictionnaire. D’autres représentations encore sont possibles.

Une illustration basique de la réduction de la dimensionnalité peut être vue dans notre exemple de reconnaissance de chiffres de la section sur la classification plus haut. Peut-être n’avions-nous pas besoin des informations de couleur pour reconnaître les chiffres; nous pourrions donc supprimer $2$ composantes de couleur et réduire la dimensionnalité de nos données de $3$ (canaux R, V, B) à $1$ (valeur en niveaux de gris). Dans la même idée, nous pourrions réduire la taille de l’image et la compresser pour réduire encore plus sa dimensionnalité.

Prenons un autre exemple: un programme qui indique si une image montre un visage ou non. Nous, humains, avons besoin de seulement quelques lignes de dessins pour reconnaître un visage. Nous pourrions donc penser intuitivement que notre algorithme n’aura besoin que d’une petite quantité des informations d’une image pour savoir s’il s’agit ou non d’un visage. Il existe en effet des réseaux de neurones capables d’extraire de telles caractéristiques d’une image et qui permettent à d’autres algorithmes de classer plus facilement l’image comme visage ou pas.

Conclusion

Il y avait beaucoup d’informations dans cet article, alors un petit récapitulatif s’impose.

Plusieurs axes sont possibles pour réaliser une taxonomie des algorithmes d’apprentissage automatique (machine learning).

Nous pouvons les différencier en fonction du type de données dont ils ont besoin pour apprendre. Dans cette taxonomie, nous avons distingué les apprentissages supervisé, semi-supervisé, non supervisé et par renforcement.

Un autre axe de taxonomie est la représentation mathématique sur laquelle ils s’appuient. De cet point de vue, nous avons distingué les techniques d’apprentissage basées respectivement sur les modèles et sur les exemples.

Une troisième possibilité consiste à différencier les algorithmes d’apprentissage automatique par la manière dont ils consomment les données d’apprentissage. Dans cet axe, nous avons des méthodes d’apprentissage par lots et les méthodes d’apprentissage incrémental.

Enfin, nous pouvons baser notre taxonomie sur le type de tâche que la fonction de prédiction résultant de l’apprentissage tentera d’effectuer. Ces tâches sont notamment la régression, la classification, le partionnement, la prise de décision, l’apprentissage de règles d’association, la séparation aveugle de source et la réduction de la dimensionnalité.

Ces différents axes de taxonomie ne sont pas exclusifs. Par exemple, un algorithme d’apprentissage supervisé peut être une technique d’apprentissage incrémental et basée sur des exemples. De plus, la taxonomie présentée dans cet article est ma tentative personnelle de relier diverses qualifications des techniques d’apprentissage automatique, et elle n’est pas exhaustive.

La taxonomie est utile lorsque nous essayons de cerner un problème et de déterminer quelle technique d’apprentissage utiliser pour ce problème en particulier. La connaissance de ces taxonomies peut nous aider à trouver un sous-ensemble réduit d’algorithmes d’apprentissage candidats parmi lesquels une technique de validation (par exemple) pourrait choisir le plus performant.

Dans le prochain article, en discutant de la régression linéaire, nous ferons un pas important vers la mise en pratique de l’apprentissage automatique.

Crédits

• [1]: Scikit learn - Multilabel classification
• [2]: Scikit learn - Demonstration of k-means assumptions
• [3]: Scikit learn - Blind source separation using FastICA
• [4]: Scikit learn - Restricted Boltzmann Machine features for digit classification
• [5]: Scikit learn - Comparison of Manifold Learning methods

Écrit le mer. 16 janv. 2019 à 12:00 GMT+00:00.
Dernière modification le dim. 10 mars 2019 à 11:18 GMT+00:00.