A sense of machine learning

Reminder: you can left-scroll and right-scroll the long math blocks

Introduction

This entry starts a series of posts that I’ll write about machine learning. We will try to acquire some of the mathematical foundations and the engineering skills it requires, but also try to get a deeper sense of what machine learning is about. I hope we acquire a clear intuition of machine learning through this post and the next ones coming.

A practical sense of machine learning

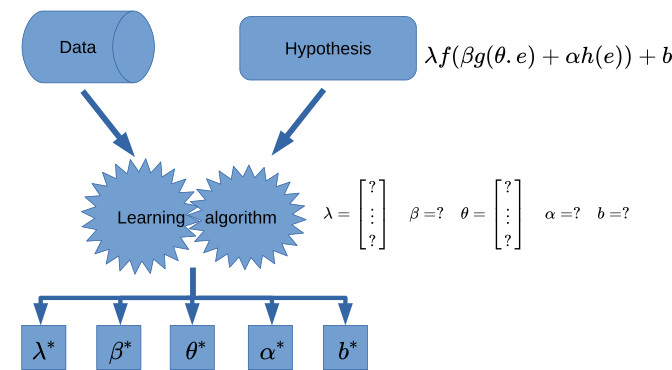
There are several definitions of machine learning from different authors. I understand machine learning as a set of techniques allowing a computer program to determine the values of the parameters of a mathematical model. The mathematical model is assumed to represent the relationships (also assumed) between elements of a data set. This figure above illustrates of this idea.

Let’s clarify the notion of “model” in our statement above. Pr Patrick H. Winston from MIT says that everything in engineering is about making models. A model is a mathematical representation of a phenomenon. For example, this intuitive description of a phenomenon: “When one pushes an object, it moves. The massive the object, the harder it is to move”, can be generalized as “When a force is applied to an object, the object is accelerated proportionally to its mass”, which was modeled by Sir Isaac Newton as the Fundamental Principle of Dynamics above:

$$\sum \vec{F} = m \vec{a}$$

Now, what did we mean by “determine the values of the parameters” of a mathematical model ? From the first paragraph above, we see that Machine Learning requires making assumptions. The first assumption is that a relationship exists between the elements of a data set we are working on. Another assumption is to choose a candidate mathematical representation (or a set of them) to model this very relationship. The candidate mathematical representation is sometime called an hypothesis.

For instance, if we think that for any element $e$ of the data set $S$, a property of interest of the data (let’s call it $e_1$) is always proportional to another property (let call it $e_2$) of this element, we will model the relationship as:

$$\forall e \in S, \quad e_1 = \beta\, e_2$$

Here, $\beta$ is the parameter of this model. If we determine $\beta$, then given any value $a_2$ that we suppose to share the rules over $S$, we can find the corresponding value $a_1 = \beta \, a_2$.

More concretely, let’s suppose the weight of a person is roughly proportional to that person’s height (not correct, but does it for our example). If we find the parameter $\beta$ corresponding to this model, we could build a software that predicts the weight of a person when it is given that person’s height.

How do we determine $\beta$ ? Well, the examples above are over-simplified, but the role of machine learning is primarily to build software packages that will determine the parameters of our models. Real life models can be quite complex and machine learning techniques will try to:

• Determine the parameters of a model from available data.
• Automatically choose between different models the one that better captures the relationships in the data.
• Determine the parameters in such a way that the model makes minimal errors on new data (data that we did not use to determine the parameters).
• etc.

So we see that Machine Learning is actually more about automatic model parameters discovery. I guess Machine Learning was a better marketing option 😃

In our paragraph about the notion of “model”, we were talking about “phenomenons” but elsewhere we talk more about “data”. What is the link between these two concepts ? Whether we are predicting the motion of a rigid body, the weather or the behaviour of customers, we are really modelling phenomenons. To do so, we rely on observations of the phenomenon, we make measurements, or in other words we collect data. We call this collected data our initial data set.

Under the hood, machine learning generally solves an optimization problem. To understand why, we must consider how we can build a software to determine the parameters of a model based on a set of data. We would select the parameters that “best fit” the data available. “Best fit” will often mean mathematically minimizing the global error that our model makes on the available data or mathematically optimizing the global gain of our model on the available data. An error function measures how much the model diverge from the expected result and a gain function measures how good the model is doing toward an objective (or goal).

Discussing our “intuition”

After reading this article, some could argue that the existence non-parametric models and of some algorithms that don’t even have a model at all contradicts the intuition we just built. However, in this article, I did not stick to the machine learning’s particular definition of the terms “parametric” and “model”. I rather tried to use them in a slightly more general sense, as shows the parallel with the model of the Fundamental Principe of Dynamics we made earlier. Sometimes in machine learning, the underlying relationships in the data set will not be addressed explicitly, but even then, I consider that we are doing an implicit approximation of the parameters of a hidden mathematical representation.

Terminology

Let’s define some terms that will come over and over again in the Machine Learning post series.

Hypothesis, model, parameters, hyper-parameters, training

Hypothesis

An hypothesis is a candidate mathematical representation of the relationships assumed to exist in the data set we are mining.

Parameters

Parameters are the constants of an hypothesis (mathematical representation of the relationships in the data set). When we pick (or assume) an hypothesis, we don’t know what actual values of these constants will best fit the available data set, so these constants are to be determine and are (paradoxically) the unknown variables of machine learning problems.

Hyper-parameters

A machine learning technique tries to determine the values of the parameters of an hypothesis. The learning technique can be algorithm that has its own parameters, for example a step size for an iterative optimization algorithm. To differentiate the parameters of the learning technique from those of the hypothesis, we call the firsts hyper-parameters. Sometimes, they also require to find a strategy to determine them as well.

Model

A model is the result of machine learning. It is the mathematical presentation (with its parameters determined) of the relationships in the data set that we will use in production on new (unmet) data instances.

Training

Training is the process of going from an hypothesis to a model, meaning the process of determining the parameters of the model based on the available data set.

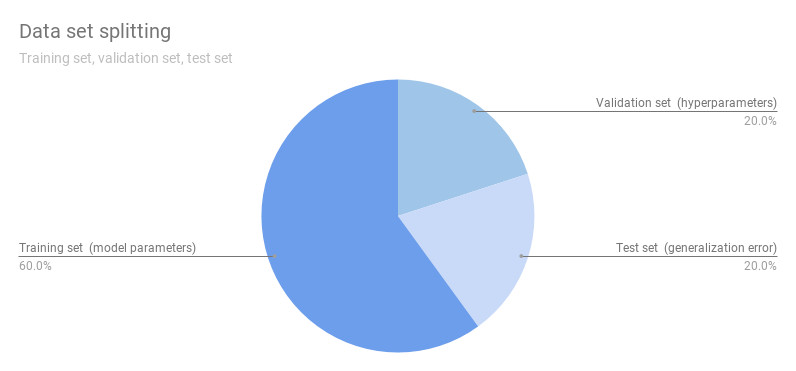
Training set, validation set, test set

Generally, we want a way to assess the model we obtain after training. To do so, we often divide the available data set into 3 disjoints subsets: a training set, a test set and a validation set. This figure above illustrates this splitting.

Training set

The training set of the part of the available data set that we will use to determine the values of the parameters of our hypothesis.

Validation set

The validation set is used to evaluate the best performing hypothesis. When we are not sure about the mathematical representation we should choose, we can use a validation set to assess different models right after training them and select the one with the lowest validation error.

We generally use a technique called cross-validation. We will explore this technique in a later post.

The validation set can also be used to fine tune the hyper-parameters of a model. In this case, for a given hypothesis, each combination of hyper-parameters is considered a different model (and assessed against all the others).

Test set

The test set is used to evaluate the generalization error of our model. It must be exclusive with the training set. Note that after assessing the model (possibly chosen using cross-validation) on the test set, we must not tweak the model anymore, as this would make the generalization error unreliable.

Conclusion

In this article, I presented my basic understanding of machine learning so far. In the short-term next posts I plan to explore the following topics:

• Taxonomy of machine learning techniques (regression, classification…).
• A sense of linear models for regression.
• Practice of machine learning of a linear model for regression.

Do you have a different insight about machine learning ? Let me know in the comments 😉

See you soon !
Keep learning !

Written on Fri Jan 4th 2019, 4:27 GMT+00:00.
Last updated on Sun Mar 10th 2019, 10:40 GMT+00:00.