Comprendre l'apprentissage automatique (machine learning)

Rappel: tu peux faire défiler à gauche et à droite les longues formules ou blocs de code.

Introduction

Ce post débute une série d’articles que j’écrirai sur l’apprentissage automatique (machine learning en anglais). Nous essaierons d’acquérir certaines des bases mathématiques et des compétences d’ingénierie que cela requiert, mais aussi de nous forger une meilleure intuition de ce qu’est l’apprentissage automatique.

Intuition pratique de l’apprentissage automatique

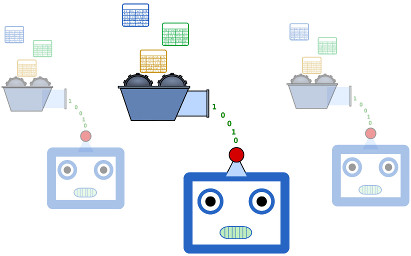
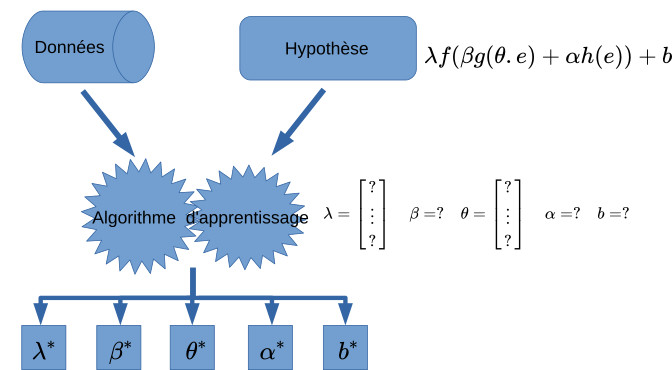
Il existe plusieurs définitions de l’apprentissage automatique données par différents auteurs. Je conçois l’apprentissage automatique comme un ensemble de techniques permettant à un programme informatique de déterminer les valeurs des paramètres d’un modèle mathématique. Le modèle mathématique est supposé représenter les relations (également supposées) entre les éléments d’un ensemble de données. Cette figure plus-bas illustre cette idée.

Clarifions la notion de “modèle” évoquée ci-dessus. Selon le Pr Patrick H. Winston du MIT, l’ingénierie consiste essentiellement en l’élaboration de modèles. Un modèle est une représentation mathématique d’un phénomène. Par exemple, cette description intuitive d’un phénomène: “Lorsqu’on pousse un objet, il se déplace. Plus un objet est massif, plus il est difficile à déplacer”, peut être généralisée en: “Lorsqu’une force est appliquée à un objet, l’objet est accéléré proportionnellement à sa masse”, ce qui a été modélisé par Sir Isaac Newton en Principe Fondamental de la Dynamique comme suit:

\sum \vec{F} = m \vec{a}

Revenons à l’apprentissage automatique. Qu’entendons-nous par “déterminer les valeurs des paramètres” d’un modèle mathématique ? De notre premier paragraphe ci-dessus, nous voyons que l’apprentissage automatique nécessite de formuler des hypothèses. La première hypothèse est qu’il existe une relation entre les éléments d’un ensemble de données sur lequel nous travaillons. Une autre hypothèse est le choix d’une représentation mathématique candidate (ou d’un ensemble d’entre elles) pour modéliser cette relation. La représentation mathématique candidate est parfois appelée hypothèse.

Par exemple, si nous pensons que pour tout élément $e$ d’un ensemble de données $S$ , une propriété d’intérêt de la donnée (appelons-la $e_1$ ) est toujours proportionnelle à une autre propriété (appelons-la $e_2$ ) de cet élément, nous modéliserons la relation comme suit:

\forall e \in S, \quad e_1 = \beta\, e_2

Ici, $\beta$ est le paramètre de ce modèle. Si nous déterminons $\beta$ , alors étant donnée une valeur quelconque $a_2$ que nous supposons partager les règles existant sur $S$ , nous pourrions trouver la valeur correspondante $a_1 = \beta \, a_2$ .

Plus concrètement, supposons que le poids d’une personne soit à peu près proportionnel à sa taille (pas correct, mais suffit pour notre exemple). Si nous trouvions le paramètre $\beta$ correspondant à ce modèle, nous pourrions construire un logiciel qui prédise le poids d’une personne lorsqu’on lui fournit sa taille.

Comment détermine-t-on $\beta$ ? Eh bien, les exemples ci-dessus sont simplifiés à l’excès, mais le rôle de l’apprentissage automatique est principalement de construire un logiciel qui déterminera les paramètres de nos modèles. Les modèles dans la vraie vie peuvent être assez complexes et les techniques d’apprentissage automatique tenteront de:

Déterminer les paramètres d’un modèle à partir des données disponibles.
Choisir automatiquement entre différents modèles celui qui capture le mieux les relations entre les données.
Déterminer les paramètres de manière à ce que le modèle commette des erreurs minimales sur les nouvelles données (données que nous n’avons pas utilisées pour déterminer les paramètres).
etc.

Nous constatons donc que l’apprentissage automatique concerne davantage la détermination automatique des paramètres des modèles. Je trouve que le nom en français, Apprentissage Automatique est plus proche de la réalité des techniques que le nom anglais Machine Learning 😃

A sense of machine learning

Dans notre paragraphe sur la notion de “modèle”, nous parlions de “phénomènes” mais ailleurs nous parlons plutôt de “données”. Quel est le lien entre ces deux concepts ? Qu’il s’agisse de prédire le déplacement d’un corps rigide, la météo ou le comportement des consommateurs, nous modélisons effectivement des phénomènes. Pour ce faire, nous nous basons sur des observations du phénomène, nous faisons des mesures, ou en d’autres termes, nous collectons des données. Nous appelons ces données collectées notre ensemble de donnnées initial.

Dans le détail, l’apprentissage automatique résout généralement un problème d’optimisation. Pour comprendre cela, nous devons examiner comment nous construirions un logiciel pour déterminer les paramètres d’un modèle en fonction d’un ensemble de données. Nous sélectionnerions les paramètres qui “correspondent le mieux” aux données disponibles. “Correspondre le mieux” signifiera souvent minimisant mathématiquement l’erreur globale que notre modèle commet sur les données disponibles ou optimisant mathématiquement le gain global de notre modèle sur les données disponibles. Une fonction d’erreur (ou de coût) mesure le degré de divergence du modèle par rapport au résultat attendu et une fonction de gain mesure le niveau de réussite du modèle par rapport à certains objectifs.

Discussion sur notre “intuition”

À la lecture de cet article, certains lecteurs pourraient arguer que l’existence de modèles non-paramétriques voire d’algorithmes d’apprentissage automatique qui n’ont pas de modèle contredit l’intuition que nous venons de nous forger. Cependant, il faut noter que dans les sections précédentes, je n’ai pas utilisé les termes “paramétrique” et “modèle” dans leurs sens stricts de l’apprentissage automatique. J’ai plutôt essayé de les employer à travers une sémantique plus générale, ainsi que l’illustre le parallèle que nous avons fait avec le modèle mathématique du Principe fondamental de la dynamique. Parfois en apprentissage automatique, les relations sous-jacentes dans l’ensemble de données ne pourrons pas être adressées explicitement, mais même dans ce cas, je considère que l’apprentissage effectue une approximation implicite des paramètres d’une représentation mathématique cachée.

Terminologie

Certains termes apparaîtront encore et encore dans la série de publications sur l’apprentissage automatique. Dans les prochaines sections nous en définissions quelques uns.

Hypothèses, modèle, paramètres, hyperparamètres, apprentissage

Hypothèse

Une hypothèse est une représentation mathématique candidate pour modéliser les relations supposées existantes dans l’ensemble de données que nous exploitons.

Paramètres

Les paramètres sont les constantes d’une hypothèse (représentation mathématique des relations existant dans l’ensemble de données). Lorsque nous sélectionnons une hypothèse, nous ne savons pas à priori quelles valeurs de ces constantes correspondront le mieux à l’ensemble de données disponible. Ces constantes doivent donc être déterminées et sont (paradoxalement) les variables inconnues des problèmes d’apprentissage automatique.

Hyperparamètres

Une technique d’apprentissage automatique tente de déterminer les valeurs des paramètres d’une hypothèse. La technique d’apprentissage peut être un algorithme qui a ses propres paramètres, comme par exemple la taille d’un pas pour un algorithme itératif d’optimisation. Pour différencier les paramètres de la technique d’apprentissage de ceux de l’hypothèse, nous appelons les premiers hyperparamètres. Parfois, il est également nécessaire de trouver une stratégie pour les déterminer.

Modèle

Un modèle est le résultat de l’apprentissage automatique. C’est la représentation mathématique (avec ses paramètres déterminés) des relations supposées exister dans le jeu de données et que nous utiliserons en production sur de nouvelles instances de données (non encore rencontrées).

Apprentissage

L’apprentissage consiste à passer d’une hypothèse à un modèle, c’est-à-dire à déterminer les valeurs des paramètres du modèle en fonction des données disponibles.

Ensemble de données d’apprentissage, ensemble de données de validation, ensemble de données de test

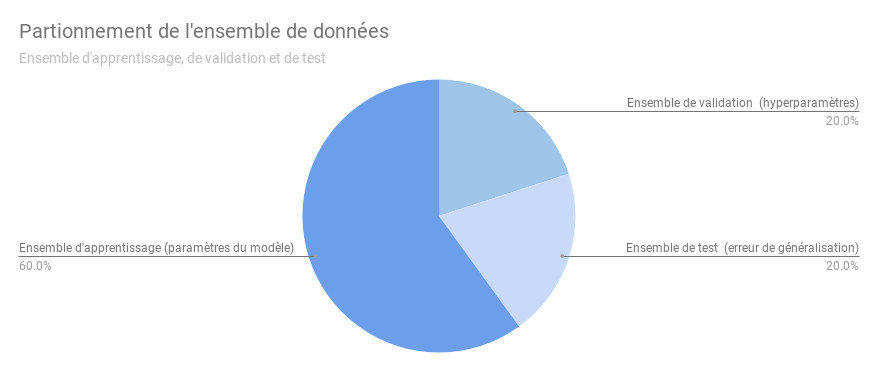
En règle générale, nous voulons avoir un moyen d’évaluer le modèle obtenu après l’apprentissage. Pour ce faire, nous pouvons diviser le jeu de données disponible en 3 sous-ensembles disjoints: un ensemble de données d’apprentissage, un ensemble de données de validation et ensemble de données de test. Cette figure plus bas illustre ce partitionnement.

Ensemble de données d’apprentissage (training set)

L’ensemble de données d’apprentissage est la partie de l’ensemble des données disponibles que nous utiliserons pour déterminer les valeurs des paramètres de notre hypothèse.

Ensemble de données de validation (validation set)

L’ensemble de données de validation est utilisé pour évaluer l’hypothèse la plus performante. Lorsque nous ne sommes pas sûrs de la représentation mathématique que nous devrions choisir, nous pouvons utiliser l’ensemble de données de validation pour évaluer différents modèles juste après les avoir entraînés et choisir celui qui présente l’erreur de validation la plus faible.

Nous utiliserons généralement une technique appelée validation croisée. Nous allons explorer cette technique dans un article à venir.

L’ensemble de données de validation peut également être utilisé pour affiner les hyperparamètres d’un modèle. Dans ce cas, pour une hypothèse donnée, chaque combinaison d’hyperparamètres est considérée comme un modèle différent (et évalué par rapport à tous les autres).

Ensemble de données de test (test set)

L’ensemble de données de test sert à évaluer l’erreur de généralisation de notre modèle. Notons qu’après avoir évalué le modèle (éventuellement choisi par validation croisée) sur l’ensemble de données de test, nous ne devons plus modifier le modèle, car cela rendrait la valeur de l’erreur de généralisation peu fiable.